How I Organize Layout Code In Swift

https://youtu.be/gZSayiwa5Ao

I was asked the other day how I organize my layout code when I am building my UI programmatically using UIKit. In this post I will walk through a variety of things that I have tried over time and end with what my typical organization now looks like. It will not teach you how auto layout works. It will also not make an argument for why you should lay out your UI this way. Different methods work for different people. If you love storyboards, run with them. All I intend to share is what I have landed on for now. (And hopefully when I look back on this article in a year, it will have further evolved, because I kept learning and growing.)

This is the layout we'll look at in these examples. All of the different pieces of code you find here should lead to this same layout.

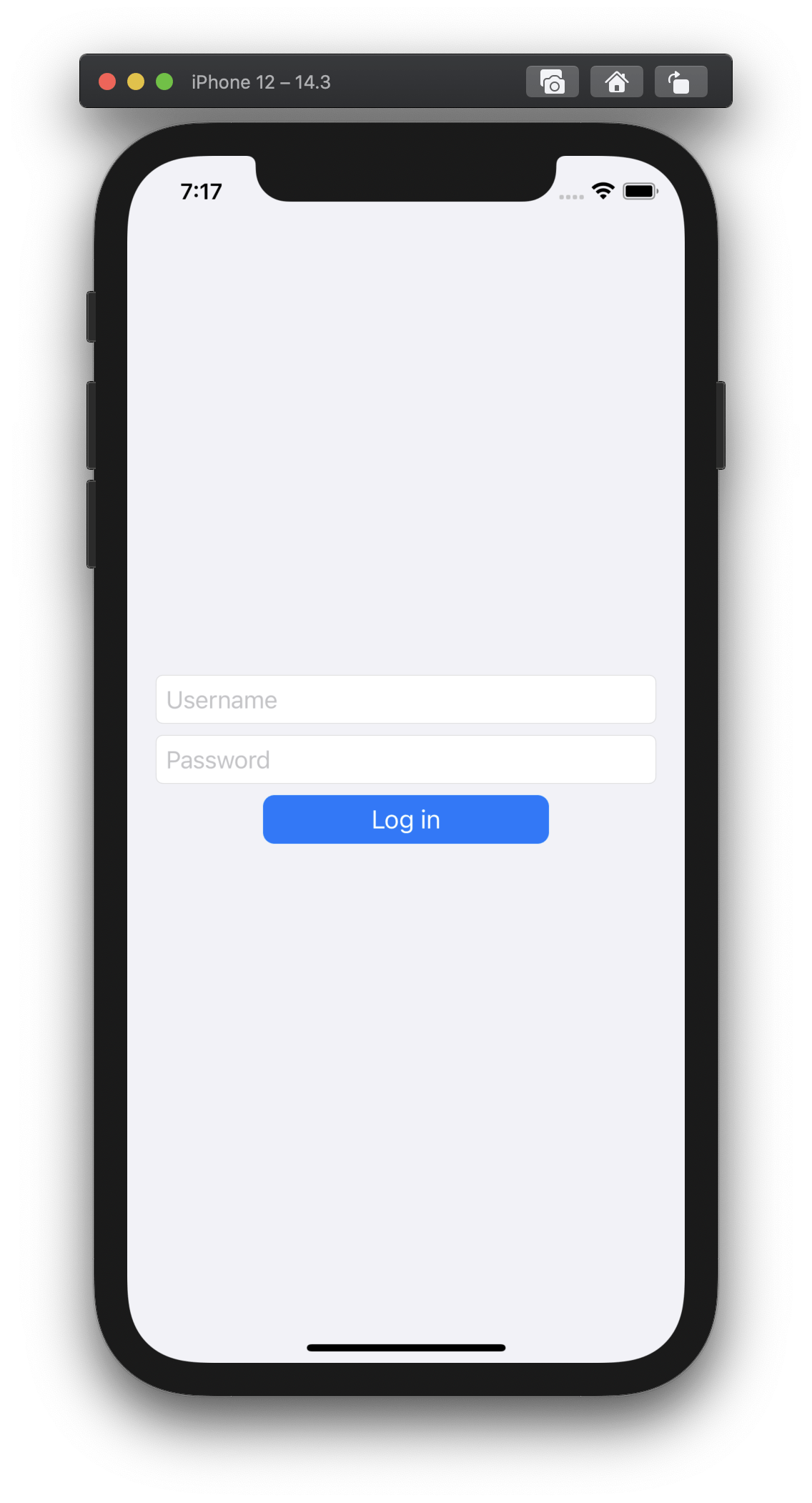
Basic Login Layout

Basic Layout

The first method I learned, and honestly what you'll see in a lot of tutorials, is to lay things out in viewDidLoad in your ViewController using a series of methods on NSLayoutAnchor called constraint. This results in code that looks like this:

class BasicLayoutViewController: UIViewController {

    // define the elements
    let usernameField = UITextField()
    let passwordField = UITextField()
    let submitButton = UIButton(type: .custom)

    override func viewDidLoad() {
        super.viewDidLoad()

         // configure them
        view.backgroundColor = .secondarySystemBackground

        usernameField.placeholder = "Username"
        usernameField.borderStyle = .roundedRect

        passwordField.placeholder = "Password"
        passwordField.textContentType = .password
        passwordField.isSecureTextEntry = true
        passwordField.borderStyle = .roundedRect

        submitButton.setTitle("Log in", for: .normal)
        submitButton.backgroundColor = .systemBlue
        submitButton.layer.cornerRadius = 8

        // add them to the view hierarchy and constrain them
        view.addSubview(usernameField)
        view.addSubview(passwordField)
        view.addSubview(submitButton)

        usernameField.translatesAutoresizingMaskIntoConstraints = false
        usernameField.leadingAnchor.constraint(equalTo: passwordField.leadingAnchor).isActive = true
        usernameField.trailingAnchor.constraint(equalTo: passwordField.trailingAnchor).isActive = true

        passwordField.translatesAutoresizingMaskIntoConstraints = false
        passwordField.topAnchor.constraint(equalTo: usernameField.bottomAnchor, constant: 8).isActive = true
        passwordField.centerYAnchor.constraint(equalTo: view.centerYAnchor).isActive = true
        passwordField.leadingAnchor.constraint(equalTo: view.leadingAnchor, constant: 20).isActive = true
        passwordField.trailingAnchor.constraint(equalTo: view.trailingAnchor, constant: -20).isActive = true

        submitButton.translatesAutoresizingMaskIntoConstraints = false
        submitButton.topAnchor.constraint(equalTo: passwordField.bottomAnchor, constant: 8).isActive = true
        submitButton.centerXAnchor.constraint(equalTo: passwordField.centerXAnchor).isActive = true
        submitButton.widthAnchor.constraint(equalToConstant: 200).isActive = true
    }
}

The first thing I started doing to improve this was to pull the configuration and constraining out to separate functions, so they are a little easier to find/digest when reading. That looks like this:

class BasicLayoutViewController: UIViewController {

    let usernameField = UITextField()
    let passwordField = UITextField()
    let submitButton = UIButton(type: .custom)

    override func viewDidLoad() {
        super.viewDidLoad()

        configure()
        constrain()
    }

    private func configure() {
        view.backgroundColor = .secondarySystemBackground

        usernameField.placeholder = "Username"
        usernameField.borderStyle = .roundedRect

        passwordField.placeholder = "Password"
        passwordField.textContentType = .password
        passwordField.isSecureTextEntry = true
        passwordField.borderStyle = .roundedRect

        submitButton.setTitle("Log in", for: .normal)
        submitButton.backgroundColor = .systemBlue
        submitButton.layer.cornerRadius = 8
    }

    private func constrain() {
        view.addSubview(usernameField)
        view.addSubview(passwordField)
        view.addSubview(submitButton)

        usernameField.translatesAutoresizingMaskIntoConstraints = false
        usernameField.leadingAnchor.constraint(equalTo: passwordField.leadingAnchor).isActive = true
        usernameField.trailingAnchor.constraint(equalTo: passwordField.trailingAnchor).isActive = true

        passwordField.translatesAutoresizingMaskIntoConstraints = false
        passwordField.topAnchor.constraint(equalTo: usernameField.bottomAnchor, constant: 8).isActive = true
        passwordField.centerYAnchor.constraint(equalTo: view.centerYAnchor).isActive = true
        passwordField.leadingAnchor.constraint(equalTo: view.leadingAnchor, constant: 20).isActive = true
        passwordField.trailingAnchor.constraint(equalTo: view.trailingAnchor, constant: -20).isActive = true

        submitButton.translatesAutoresizingMaskIntoConstraints = false
        submitButton.topAnchor.constraint(equalTo: passwordField.bottomAnchor, constant: 8).isActive = true
        submitButton.centerXAnchor.constraint(equalTo: passwordField.centerXAnchor).isActive = true
        submitButton.widthAnchor.constraint(equalToConstant: 200).isActive = true
    }
}

I also went through a phase where all my UI elements were lazy and the configuration was done in a closure. I don't do that anymore mostly because I prefer to keep all my configuration code together and to abstract out commonly used configurations, but when I did it looked something like this:

private lazy var usernameField: UITextField = {
    let textField = UITextField()
    textField.placeholder = "Username"
    textField.borderStyle = .roundedRect
    return textField
}()

Moving Out Of The View Controller

The next step was hearing in some conference talk that you should do the view stuff in the view, not the view controller. That made a lot of sense to me, so I started defining custom views like this:

class BasicLayoutView: UIView {

    private let usernameField = UITextField()
    private let passwordField = UITextField()
    private let submitButton = UIButton(type: .custom)

    override init(frame: CGRect) {
        super.init(frame: frame)

        configure()
        constrain()
    }

    required init?(coder: NSCoder) {
        fatalError("init(coder:) has not been implemented")
    }

    func configure() {
        backgroundColor = .secondarySystemBackground

        usernameField.placeholder = "Username"
        usernameField.borderStyle = .roundedRect

        passwordField.placeholder = "Password"
        passwordField.textContentType = .password
        passwordField.isSecureTextEntry = true
        passwordField.borderStyle = .roundedRect

        submitButton.setTitle("Log in", for: .normal)
        submitButton.backgroundColor = .systemBlue
        submitButton.layer.cornerRadius = 8
    }

    func constrain() {
        addSubview(usernameField)
        addSubview(passwordField)
        addSubview(submitButton)

        usernameField.translatesAutoresizingMaskIntoConstraints = false
        usernameField.leadingAnchor.constraint(equalTo: passwordField.leadingAnchor).isActive = true
        usernameField.trailingAnchor.constraint(equalTo: passwordField.trailingAnchor).isActive = true

        passwordField.translatesAutoresizingMaskIntoConstraints = false
        passwordField.topAnchor.constraint(equalTo: usernameField.bottomAnchor, constant: 8).isActive = true
        passwordField.centerYAnchor.constraint(equalTo: centerYAnchor).isActive = true
        passwordField.leadingAnchor.constraint(equalTo: leadingAnchor, constant: 20).isActive = true
        passwordField.trailingAnchor.constraint(equalTo: trailingAnchor, constant: -20).isActive = true

        submitButton.translatesAutoresizingMaskIntoConstraints = false
        submitButton.topAnchor.constraint(equalTo: passwordField.bottomAnchor, constant: 8).isActive = true
        submitButton.centerXAnchor.constraint(equalTo: passwordField.centerXAnchor).isActive = true
        submitButton.widthAnchor.constraint(equalToConstant: 200).isActive = true
    }
}

And the view controller would load the view like this:

class BasicLayoutViewController: UIViewController {

    // the contentView is lazily loaded so that all the work of initializing our view
    // isn't done until the view controller is actually ready to load it
    lazy var contentView: BasicLayoutView = .init()

    override func loadView() {
        view = contentView
    }
}

This works pretty well. It gets the layout into the view, and keeps the view controller pretty clean so that it is easier to find/read/add business logic there. One thing I didn't like though was that I had to provide the required init?(coder:) in all of my views, even though I wasn't using it for anything. It just cluttered up my code and added boilerplate. So I decided to add a new UIView subclass to act as the parent for classes that I intended to layout programmatically. It looks like this:

class ProgrammaticView: UIView {
    @available(*, unavailable, message: "Don't use init(coder:), override init(frame:) instead")
    required init?(coder: NSCoder) {
        fatalError("init(coder:) has not been implemented")
    }

    override init(frame: CGRect) {
        super.init(frame: frame)

        configure()
        constrain()
    }

    func configure() {}
    func constrain() {}
}

Marking the required initializer as unavailable makes it so that you don't have to provide it in subclasses. You can see that I've also defined some template methods for configure() and constrain() and called those in the initalizer. That makes BasicLayoutView look like this:

class BasicLayoutView: ProgrammaticView {

    private let usernameField = UITextField()
    private let passwordField = UITextField()
    private let submitButton = UIButton(type: .custom)

    override func configure() {
        // same as before...
    }

    override func constrain() {
        // same as before...
    }
}

Much nicer. The view that it inherits from tells you that it is intended to be laid out programmatically, and all the code written in this class is relevant to it. You just have to add override to the configure and constrain methods.

Cleaning Up

Next, I learned about NSLayout.activate() which takes an array of NSLayoutConstraints and activates them all at once. This might be more efficient in certain cases, but it mostly means that you don't have to write .isActive = true for every constraint. I also added a couple of convenience extensions to UIView to redeuce the number of lines I have to write for every view. That looks like this:

extension UIView {
    func addConstrainedSubview(_ view: UIView) {
        view.translatesAutoresizingMaskIntoConstraints = false
        addSubview(view)
    }

    func addConstrainedSubviews(_ views: UIView...) {
        views.forEach { view in addConstrainedSubview(view) }
    }
}

// in BasicLayoutView
override func constrain() {
    addConstrainedSubviews(usernameField, passwordField, submitButton)

    NSLayoutConstraint.activate([
        usernameField.leadingAnchor.constraint(equalTo: passwordField.leadingAnchor),
        usernameField.trailingAnchor.constraint(equalTo: passwordField.trailingAnchor),

        passwordField.topAnchor.constraint(equalTo: usernameField.bottomAnchor, constant: 8),
        passwordField.centerYAnchor.constraint(equalTo: centerYAnchor),
        passwordField.leadingAnchor.constraint(equalTo: leadingAnchor, constant: 20),
        passwordField.trailingAnchor.constraint(equalTo: trailingAnchor, constant: -20),

        submitButton.topAnchor.constraint(equalTo: passwordField.bottomAnchor, constant: 8),
        submitButton.centerXAnchor.constraint(equalTo: passwordField.centerXAnchor),
        submitButton.widthAnchor.constraint(equalToConstant: 200),
    ])
}

That is both shorter and a little bit easier to read. Again, putting the information that is relevant to this view in the view and striping out noise that we don't really care about.

Next, I started throwing UIStackViews into the mix whenever I could. I added another convenience method specific to stack views too. For this view that would look like this:

extension UIStackView {
    func addArrangedSubviews(_ views: UIView...) {
        views.forEach { view in addArrangedSubview(view) }
    }
}

class StackViewLayoutView: ProgrammaticView {
    private let stackView = UIStackView()
    private let usernameField = UITextField()
    private let passwordField = UITextField()
    private let submitButton = UIButton(type: .custom)

    override func configure() {
        // same stuff as before...

        stackView.axis = .vertical
        stackView.spacing = 8
        stackView.alignment = .center
    }

    override func constrain() {
        addConstrainedSubview(stackView)
        stackView.addArrangedSubviews(usernameField, passwordField, submitButton)

        NSLayoutConstraint.activate([
            stackView.leadingAnchor.constraint(equalTo: leadingAnchor, constant: 20),
            stackView.trailingAnchor.constraint(equalTo: trailingAnchor, constant: -20),
            stackView.centerYAnchor.constraint(equalTo: centerYAnchor),

            passwordField.widthAnchor.constraint(equalTo: stackView.widthAnchor),
            usernameField.widthAnchor.constraint(equalTo: stackView.widthAnchor),
            submitButton.widthAnchor.constraint(equalToConstant: 200),
        ])
    }
}

Anchorage

Already that is a lot cleaner than where we started and it is pretty flexible in terms of defining a variety of layouts in a fairly concise way. But I usually go a step farther when I am in a context where I can pull in third party dependencies. My favorite library for working with constraints is called Anchorage. It lets you write constraints with operators and provides some convenient proxies for doing things like setting all the sides at once or the size or whatever. It is fast to write and very easy to read. It's main downside is increased compile time, but it isn't really noticeable unless you're in a giant project and they are doing work to improve that.

Rewriting our view with Anchorage would look like this:

class AnchorageLayoutView: ProgrammaticView {
    private let usernameField = UITextField()
    private let passwordField = UITextField()
    private let submitButton = UIButton(type: .custom)

    override func configure() {
        // same as before...
    }

    override func constrain() {
        addSubviews(usernameField, passwordField, submitButton)

        passwordField.centerYAnchor == centerYAnchor
        // notice you can constrain the leading and trailing anchors at the same time
        passwordField.horizontalAnchors == horizontalAnchors + 20

        usernameField.bottomAnchor == passwordField.topAnchor - 8
        usernameField.horizontalAnchors == passwordField.horizontalAnchors

        submitButton.topAnchor == passwordField.bottomAnchor + 8
        submitButton.centerXAnchor == passwordField.centerXAnchor
        submitButton.widthAnchor == 200
    }
}

Like I said, it looks super clean and is very easy to read and write.

Putting It All Together

Finally, I started to combine Anchorage with stackviews, and compose them both with views defined elsewhere. This is closest to what my actual method is at this point in time. Basically any time I have a view that can be reused, I'll pull it out to its own ProgrammaticView subclass and then just plug it into views where it is needed like we've been doing with UITextFields and UIButtons in this example layout. With our example layout, that might look something like this:

class LoginStackView: ProgrammaticView {
    private let stackView = UIStackView()
    private let usernameField = UITextField()
    private let passwordField = UITextField()
    private let submitButton = UIButton(type: .custom)

    override func configure() {
        // same as before...
    }

    override func constrain() {
        addSubview(stackView)
        stackView.addArrangedSubviews(usernameField, passwordField, submitButton)

        stackView.edgeAnchors == edgeAnchors
        passwordField.horizontalAnchors == horizontalAnchors
        usernameField.horizontalAnchors == horizontalAnchors
        submitButton.widthAnchor == 200
    }
}

class ComposedLayoutView: ProgrammaticView {
    private let loginStack = LoginStackView()

    override func configure() {
        backgroundColor = .secondarySystemBackground
    }

    override func constrain() {
        addSubview(loginStack)

        loginStack.horizontalAnchors == horizontalAnchors + 20
        loginStack.centerYAnchor == centerYAnchor
    }
}

Pulling out the login stack to its own view may or may not be worthwhile. It would depend on how often you foresee using this specific view throughout your app. If you needed to, you could make it more configurable so that it could be reused in a wider variety of use cases. Either way, I think it illustrates the technique well.

Side note, you may be wondering how I pass information back up from all the subviews to the view controller. My last article on delegation describes exactly my process for that, so I won't go into it here.

Wrap Up

There you have it. That is basically the journey I took from first learning how to define a constraint in code to how I organize that code today. When you get down to it, what that code is doing is almost exactly the same, but I think the method I have now is easier to read (both for myself and others), it is easier to reuse, and it is faster to get something built because I don't have to remember any of the unimportant noise. I hope it has been helpful to you and maybe given you an idea or two that you can try applying in your own code. If you have questions, or ideas for how I can improve things let me know in the comments!

You can find all the code and the sample project I built for this article at this github repo.

How I Organize Layout Code In Swift

Comments

More from this blog

Completion Handlers in Swift

My Journey Into App Development

Xcode Tip: Pre-Build Actions

Stop Throwing Away Errors

5 Reasons To Use Typealias

Basic Layout

Moving Out Of The View Controller

Cleaning Up

Anchorage

Putting It All Together

Wrap Up

Command Palette

Comments

More from this blog

Basic Layout

Moving Out Of The View Controller

Cleaning Up

Anchorage

Putting It All Together

Wrap Up